Dungeon Generation 1

21/7/2020

Tal y como se ha explorado aquí, una forma de crear mejor contenido generado proceduralmente es imitar el procedimiento que sigue un diseñador. En el caso de generar la dungeon de un videojuego es extremadamente complejo. Entre otras cosas, hay que tener en cuenta: Topología de la dungeon, puzzles, distribución de enemigos, distribución de objetos y recompensas, estilo artístico, verificar que sea posible completarlo… Son tantas cosas que sería imposible hacerlo solo de una vez. Además, la naturaleza de cada una de esas propiedades son muy distintas, así que sería apropiado usar distintas técnicas de PCG. Por ello, una buena solución usar una técnica de generación secuencial, de forma que primero se crean los componentes más abstractos, y luego los siguientes componentes que construyen sobre los anterioes.

El primer nivel en la generación podría ser la topología o grafo. Suponiendo que la dungeon está compuesta por habitaciones y pasillos, los nodos del grafo serán las habitaciones y las aristas los pasillos. Además, haremos que el grafo sea en formato de árbol ya que es más simple. En el futuro lo haré para que incorpore ciclos usando reglas que se explican aquí. Pero aquí solamente se tendrán en cuenta las siguientes propiedades:

Formato de árbol.
Grafo conexo.
Grafo planar.
Máximo 4 aristas por nodo.
Del nodo inicial salen 3 aristas.
Existen puertas cerradas con llave.
Existen nodos que contienen llaves.
Las llaves se tienen que poder coger antes que atravesar la puerta.

A continuación de muestra un ejemplo de grafo que generaría. El nodo inicial del árbol será el inicio de la dungeon y el nodo final estará en una de las ramas. Los nodos que se encuentran entre el inicio y el final forman parte del camino principal, y todas las demás ramas son caminos secundarios. Al existir puertas cerradas, el jugador tendrá que explorar ramas secundarias para poder completar la dungeon. Las aristas rojas son puertas cerradas, y los nodos rojos contienen la llave. De esta forma, solamente las ramas con llaves son obligatorias para completar la dungeon, mientras que las otras ramas opcionales pueden contener recompensas para el jugador.

Para hacer que la dungeon sea de dificultad creciente al explorarla, se puede asignar un número a cada uno de los nodos que determina la dificultad de la sala, el cual puede ser simplemente su distancia con el nodo inicial. De esta forma, una etapa posterior de PCG puede elegir qué enemigos y objetos poner en la sala en función de su dificultad.

Por cierto, con “llave” en este grafo se entiende cualquier cosa capaz de desbloquear una arista, es una abstracción. A nivel de implementación, podría ser una habilidad que adquiere el jugador, una palanca con un puzzle que abre una puerta, recibir ayuda de un npc que le desbloquee el camino, reducir el nivel de peligro matando a todos los enemigos de la sala, o cualquier cosa imaginable que cumpla esa función.

graphDiagram1

Para generar la dungeon estaría bien poder controlar una serie de parámetros como el número de nodos, de llaves, de ramas, y una distancia mínima entre inicio y final. En clingo se puede codificar todo esto usando constantes:

0
1
2
3
4
5
6
7
8


 
#const maxDistance=10.
#const minFinishDistance=4.
#const maxFinishDistance=8.
#const minNodes=15.
#const maxNodes=20.
#const minNumLeafs=5.
#const maxNumLeafs=9.
#const numKeys=3.

En vez de dar un número fijo, se codifican rangos en algunos valores para que que a clingo le sea más facil encontrar la solución, además de que podría no encontrar una solución con parámetros fijos. Los predicados más importantes son:

node/1: Indica qué nodos existen.
edge/2: Qué aristas hay entre 2 nodos.
connected/2: Qué nodos están conectados.
adyacent/2: Qué nodos son adyacentes, sin importar la dirección de la arista.
distance/3: La distancia que hay entre 2 nodos.
leafNode/1: Qué nodos son hojas del árbol.
key/1: Qué llaves hay.
edgeKey/3: Qué llave tiene asociada una arista.
nodeKey/2: Qué llave tiene asociado un nodo.

Para la codificación del programa se ha usado el método de Generate y Restriction: Primero se generan todas las posibles soluciones, y luego se eligen entre todas ellas a través de restriciones. Además, hay un pequeño codigo python agregado que permite visualizar de forma rápida el resultado (es necesario tener graphviz para ello). Para la generación de llaves lo que se hace es dividir el grafo en áreas, con las aristas con puertas separándolas. Se etiquetan esas áreas en función de la llave asociada a la puerta, para luego obligar que esa misma llave esté en la misma área que su puerta correspondiente. A parte del código, tambien se muestra una imagen del resultado que da.

  0
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121


 
#script (python)
import clingo
import graphviz as gv


def writeAtom(atom, g):
	if(atom.name == "edgeNormal"):
		node1 = str(atom.arguments[0])
		node2 = str(atom.arguments[1])
		g.edge(node1, node2)
	elif(atom.name == "edgeKey"):
		node1 = str(atom.arguments[0])
		node2 = str(atom.arguments[1])
		g.edge(node1, node2, color="blue")

	elif(atom.name == "nodeKey"):
		node = str(atom.arguments[0])
		g.node(node, color="blue")

def main(prg):
	g = gv.Digraph('G', filename='grafo.gv')
	prg.ground([("base", [])])
	with prg.solve(yield_=True) as h:
		for m in h:
			for atom in m.symbols(atoms=True):
				writeAtom(atom, g)
	g.view()
#end.

#const maxDistance=10.
#const minFinishDistance=4.
#const maxFinishDistance=8.

#const minNodes=5.
#const maxNodes=20.

#const minNumLeafs=3.
#const maxNumLeafs=8.

#const numKeys=3.

%El nodo 0 es el inicio y el 1 el final

node(0).
node(1).
minNodes {node(2..maxNodes+2)}.  
{edge(N1, N2): node(N1), node(N2), N1!=N2}.


connected(N1, N2) :- edge(N1, N2).
connected(N1, N3) :- connected(N1, N2), connected(N2, N3).

adyacent(N1, N2) :- edge(N1, N2).
adyacent(N2, N1) :- adyacent(N1, N2).

distNum(1..maxDistance).
1 {distance(0, N, D): distNum(D)} 1 :- node(N), N!=0.

%Deducir que nodos son leaf.
leafNode(N) :- node(N), 0 {edge(N, N2): node(N2)} 0.

%%%%%%%%%%%%%%%%%%%%%%%%%%%% Keys %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
key(1..numKeys).
numKeys {edgeKey(N1, N2, K): edge(N1, N2), key(K)} numKeys.
edgeNormal(N1, N2) :- edge(N1, N2), not edgeKey(N1, N2, K):key(K).
numKeys {nodeKey(N, K): node(N), key(K), N!=0, N!=1} numKeys.

nodeTag(0, 0).
nodeTag(N2, T) :- nodeTag(N1, T), edgeNormal(N1, N2). 
nodeTag(N2, K) :- edgeKey(_, N2, K).

%Dividir el grafo en areas, con las puertas con llave separando cada area
%:-node(N), not 1 {nodeTag(N,K):nodeTag(N,K)} 1.

%Las llaves estan antes de cruzar su respectiva puerta
:-edgeKey(N1, N2, K), nodeTag(N1, T), nodeKey(N3, K), not nodeTag(N3, T).

%Todas las puertas con llave estan en el camino principal
:-edgeKey(_, N, _), not connected(N, 1).

%Todos los nodos con llave son leaf
:-nodeKey(N, _), not leafNode(N).

%Solo una llave por nodo
:-node(N), not 0{nodeKey(N, K): nodeKey(N, K)}1.

%Tiene que haber una llave de cada
:-key(K), not 1{nodeKey(N, K): nodeKey(N, K)}1.

%%%%%%%%%%%%%%%%%%%%%%%%%%%% Restrictions %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%Calculo de distancias
:-edge(0, N), not distance(0, N, 1).
:-distance(0, N1, D), edge(N1, N2), not distance(0, N2, D+1).

%Una sola arista entre dos nodos
:-edge(N1, N2), edge(N2, N1). 

%El grafo tiene que ser conexo.
:-node(N), N!=0, not connected(0, N).

%El inicio y el final tienen que estar conectados
:-not connected(0, 1).

%Maximo 4 conexiones en cada nodo
:-node(N1), {adyacent(N1, N2) : adyacent(N1, N2)} > 4.

%3 adyacentes al nodo inicial
:-not 3 {edge(0, N) : edge(0, N)} 3.

%Obligar un rango de distancias entre inicio y final
:-distance(0, 1, D), not D>=minFinishDistance, not D<=maxFinishDistance.

%Obligar un rango de nodos leaf
:-not minNumLeafs {leafNode(N): leafNode(N)} maxNumLeafs.

%Obligar que el nodo final sea leaf
:- not leafNode(1).

%Obligar que el grafo sea un arbol
:-node(N), not 0 {edge(N2, N): edge(N2, N)} 1.

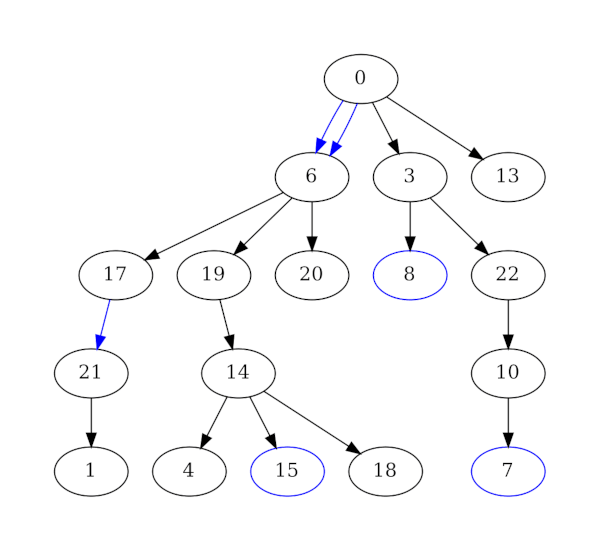
Si se ejecuta el código tal cual con los mismos parámetros, Clingo siempre dará el mismo resultado, lo cual no es muy deseable para un sistema de PCG. Por eso, se puede llamar por ejemplo con los parámetros “–sign-def=rnd –rand-freq=0.2 –seed=732719” para que genere grafos de forma aleatoria en función de la seed proporcionada. Se podrían añadir más reglas para perfeccionar los resultados, pero tal como está ahora es demasiado lento. En mi máquina tarda entre 20 segundos y varios minutos en función de los parámetros, lo cual es inaceptable si se quiere poner este sistema en un videojuego rogue like. Por ello, en el siguiente artículo codificaré este mismo generador pero haciendo uso de clingo multi-shot. Con este método la solución se construye por partes en vez de toda de una vez, lo cual lo hace más eficiente.