Diseño de un healer de un RPG usando lógica difusa

20/1/2023

Introducción

Imagínate que estas implementando la inteligencia artificial de un agente en un RPG. Es posible que uno de los agentes tome el rol de un healer, el cuál puede realizar acciones tales como curar a un aliado, aplicar un buff, o atacar al enemigo. Como jugador, es intuitivo cuál es el trabajo que debería de hacer el healer: curar aliados cuando están bajos de vida, aplicar los buffs cuando son una ventaja contra el enemigo en especifico, huir del enemigo si está siendo atacado… Sin embargo, todas estas reglas las piensas en lenguaje natural y en términos imprecisos. Si quieres implementar un agente que las ejecute necesitarías usar técnicas como arboles de decisión o, si es lo suficientemente simple, a mano con simples if condicionales. Sin embargo, hay una técnica que te permite traducir casi literalmente la “intuición” de cómo debería de funcionar un healer en términos que un computador las entienda. Algo como lo siguiente:

IF companion health IS low THEN heal companion.
IF enemy resistance to fire IS low THEN apply fire buff to companion.
IF healer being attacked IS high THEN retreat.

Estas reglas son muy fáciles de entender ya que son casi en lenguaje natural, con lo que sería fácil el añadir nuevas reglas o modificar las que ya existen. El cuerpo del if corresponde a la condición necesaria para que se cumpla, lo cual el agente extraería de algún sensor, mientras que el then corresponde a la acción que realizaría el agente. La técnica que nos permite usar reglas de este tipo se llama fuzzy logic. Es fuzzy (difuso) porque en las reglas se utilizan términos imprecisos como low, medium o high. Esto permite que las reglas sean capaces de adaptarse en entornos continuos como un videojuego.

Por ejemplo, el concepto de que un enemigo sea débil a fuego no es tanto un valor booleano, sino más bien algo difuso que dependería del valor numérico en específico. Si la resistencia puede ser un valor entre 0 y 100, ¿es un valor de 10 débil al fuego? ¿y 40? Quizás, o quizás no. Fuzzy logic es capaz de razonar en términos imprecisos como este.

Algo importante a tener en cuenta es que un uso directo de fuzzy logic implementa un Reactive agent, es decir, la decisión que toma es computada únicamente a partir de sus sensores en su estado actual. No aplica ningún tipo de planificación ni almacena un historial de anteriores estados del entorno. Sin embargo, es posible utilizar razonamiento de fuzzy logic en un systema más complejo que sí incorpore planificación, como GOAP (Goal-Oriented Action Planning).

Fuzzifization

Como he dicho anteriormente, fuzzy logic no usa valores de true/false, sino un elemento llamado fuzzy set. Un elemento pertenece a un fuzzy set con un grado de membresía continuo entre 0 y 1. Por ejemplo, si en un videojuego tienes el concepto health en un personaje que puede tener un valor entre 0 y 300, lo podrías dividir, por ejemplo, en 3 fuzzy sets: “low_health”, “medium_health” y “high_health”, con unos valores de membresía en cada uno de los sets dependiente del valor de health actual del personaje. Un posible mapping es si la vida del personaje es 36, low_health podría tener un valor de 0.9, medium_health de 0.12, y high_health de 0. Como puedes observar, es posible tener un valor de pertenencia en múltiples sets, aunque sea low_health el más probable de ellos. Ahora la pregunta es, ¿como puedo computar los valores de membresía a partir de un valor real? Se usan principalmente 2 functiones: triangular y trapezoidal. Se pueden utilizar otras funciones más exóticas como gaussiana, pero el alto coste de computarla normalmente no hace que valga la pena su uso. En las siguientes imágenes se muestra un ejemplo de funciones triangular y trapezoidal (observa como el input es entre 0 y 1, por lo que sería necesario normalizar el valor real health de 0-300 a 0-1):

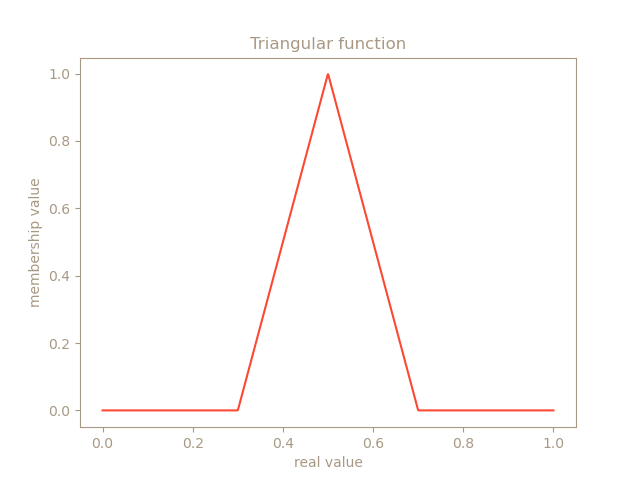
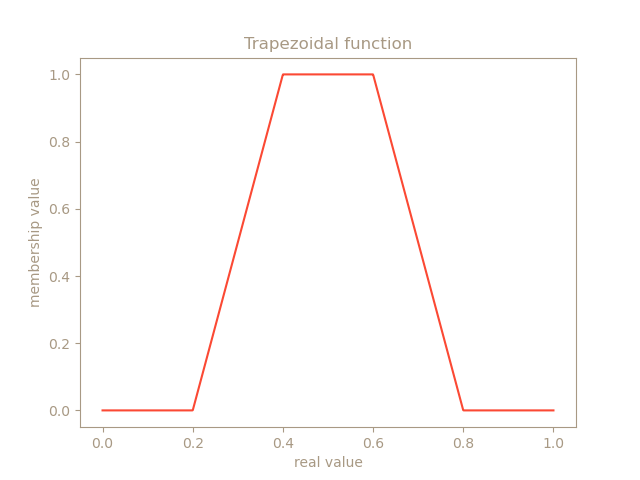
triangular function trapezoidal function

El siguiente pseudocódigo muestra un ejemplo de cómo se podría computar las funciones triangular y trapezoidal. La función triangular solo necesita 3 valores: En dónde en el X axis se encuentra el borde izquierdo, el pico y el borde derecho. La función trapezoidal en vez de un único valor pico, usa un valor de pico izquierdo y derecho.


function createRectFunction(point1, point2) return slope, y_intercept
    slope ← (point2[1] - point1[1]) / (point2[0] - point1[0])
    y_intercept ← point1[1] - (slope * point1[0])
    return (slope, y_intercept)
end function

function triangularFunction(x, left, peak, right) return y
    (left_slope, left_intercept) ← createRectFunction((left, 0.), (peak, 1.))
    (right_slope, right_intercept) ← createRectFunction((peak, 1.), (right, 0.))
    if(x <= left) then
        y ← 0.
    else if(x <= peak) then
        y ← x * left_slope + left_intercept
    else if(x <= right) then
        y ← x * right_slope + right_intercept
    else
        y ← 0.
    return y
end function

function trapezoidalFunction(x, left, leftPeak, rightPeak, right) return y
    (left_slope, left_intercept) ← createRectFunction((left, 0.), (leftPeak, 1.))
    (right_slope, right_intercept) ← createRectFunction((rightPeak, 1.), (right, 0.))
    if(x <= left) then
        y ← 0.
    else if(x <= leftPeak) then
        y ← x * left_slope + left_intercept
    else if(x <= rightPeak) then
        y ← 1.
    else if(x <= right) then
        y ← x * right_slope + right_intercept
    else
        y ← 0.
    return y
end function

En un caso de uso real normalmente se divide un valor real de entrada en múltiples fuzzy sets, como sea ha hecho anteriormente con low, medium y high sets de health. Para ello, normalmente se distribuyen las funciones de membresía en el rango 0-1 de forma que haya solapamiento entre ellas, como se observa en la siguiente imagen:

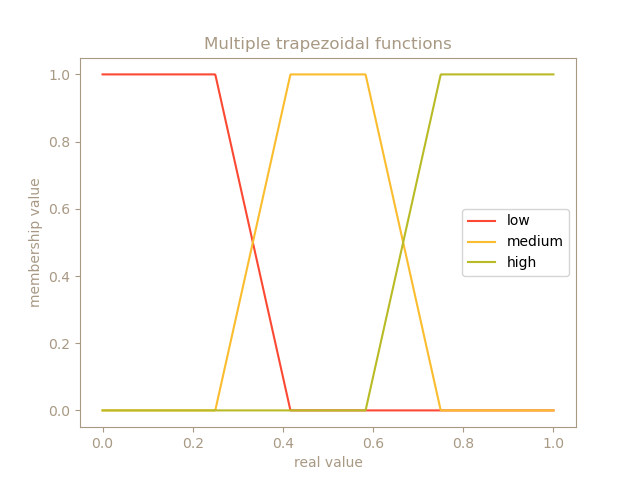
triangular function

Para cada uno de los sensores y acciones, es necesario crear multiples fuzzy sets para cada uno de ellos. Se han creado 3 para health, pero se podrían crear también 4 para un concepto que determine el nivel de peligro del personaje, otros 3 para la acción de curar a un aliado, etc. La decisión de qué función de membresía utilizar y cuántos fuzzy sets crear para cada concepto es una decisión de diseño. Que haya solapamiento entre los fuzzy sets es importante porque es lo que permite la inferencia con valores imprecisos. Sino, el algoritmo degenera en un sistema de lógica booleana.

El siguiente pseudocódigo es capaz de computar las funciones de membresía indicando en cuántos fuzzy sets quieres particionar el espacio y cuánto solapamiento entre ellas, siendo un valor entre 0 y 1.


function createTrapezoidalFuzzySets(fuzzySetCount, overlappingAmount) return list
    listOfTuples ← empty list
    leftPeak ← null
    rightPeak ← null
    leftBound ← null
    rightBound ← null
    overlap ← overlappingAmount / (fuzzySetCount * 2)
    for i ← 0 to fuzzySetCount do
        if( i == 0):
            leftBound ← 0. - 0.01
            leftPeak ←  0.
        else:
            leftBound  ← i / fuzzy_set_count - overlap
            leftPeak   ← i / fuzzy_set_count + overlap
        if(i >= fuzzySetCount - 1):
            rightBound ← 1.01
            rightPeak  ← 1.
        else:
            rightBound ← (i + 1) / fuzzy_set_count + overlap
            rightPeak  ← (i + 1) / fuzzy_set_count - overlap
        listOfTuples.add((leftBound, leftPeak, rightPeak, rightBound))
    return listOfTuples
end function

function createTriangularFuzzySets(fuzzySetCount, overlappingAmount) return list
    listOfTuples ← empty list
    pointCount ← fuzzySetCount * 2 - 2
    peak ← null
    leftBound ← null
    rightBound ← null
    for i ← 0 to fuzzySetCount - 1 do
        peak       ← i * 2 / pointCount
        leftBound  ← (i * 2 - 1) / pointCount - overlappingAmount / 2
        rightBound ← (i * 2 + 1) / pointCount + overlappingAmount / 2
        listOfTuples.add((leftBound, peak, rightBound))
    return listOfTuples
end function

Reglas de fuzzy logic

Una vez que hemos computado los fuzzy sets de entrada a partir de los sensores del agente, ahora es necesario computar los fuzzy sets de salida. Para ello se utilizan reglas logicas con las siguientes operationes: and, or, not, →. El operador → se llama condicional, su parte izquierda se llama body y la parte derecha head. Para que la inferencia sea correcta, todos los fuzzy sets definidos deben de aparecer como mínimo en una regla lógica. Los fuzzy sets que únicamente aparecen en el cuerpo de las reglas se denominan de entrada, y los que aparecen en la cabeza son de salida. Es necesario aplicar el proceso de fuzzification para todos los fuzzy sets de entrada, pero no para los de salida. El cómputo de las expresiones es con las siguientes fórmulas:

A and B: min(A, B)
A or B: max(A, B)
not A: 1 - A
A → set: set = A

Estás fórmulas son solo unas de tantas que se pueden aplicar. Otras opciones son el producto algebraico, suma algebraica, drastic product, drastic sum, etc…

El caso del operador de implicación es especial, dado que es el único capaz de modificar el valor de membresía de un fuzzy set. El head de la implicación es obligatorio que sea un fuzzy set, mientras que en cualquier otro caso en las expresiones donde aparece A o B, pueden ser fuzzy sets u otras expresiones lógicas. En el caso de que hayan múltiples reglas lógicas que modifiquen el mismo fuzzy set en el head de la regla, se escoge el valor máximo entre ellos.

Un problema que puede surgir es en el caso de las reglas transitivas. Si tienes por ejemplo las reglas “a → b” y “b → c”, el orden en el que se computan es importante. No existe ningún valor de membresía en el fuzzy set b hasta que se computa la primera regla. Una primera solución es simple, solamente tienes que insertar las reglas en el orden correcto en el sistema, pero no es del todo satisfactoria. Si hay muchas reglas es muy fácil que una persona se equivoque y sería muy difícil detectar el error.

Una solución más robusta al problema de las reglas transitivas es utilizar un algoritmo de ordenamiento topológico. Primero es necesario explorar todas las reglas y crear a partir de ellas un grafo de dependencia entre los fuzzy sets. Para cada regla, para cada fuzzy set que aparece en el cuerpo de la regla, se crea una arista hacia el fuzzy set del head. Luego de computar el grafo de dependencias, se crea un vector ordenado de los fuzzy sets a partir de este grafo de dependencias utilizando ordenamiento topológico. Por último, ordenar las reglas comparando los head según su posición en este vector ordenado. Aunque todo este proceso pueda parecer costoso computacionalmente, solo es necesario hacerlo una vez cuando se está creando el sistema. Además, tampoco es necesario usarlo ni implementarlo si sabes que no vas a utilizar reglas transitivas o si crees que es lo suficientemente simple como para que ordenarlas manualmente sea factible.

Defuzzification

Una vez que se ha computado el valor de membresía para todos los fuzzy sets de salida, el último paso es aplicar defuzzification. Esto nos permite obtener un valor real a partir del valor de membresía de múltiples fuzzy sets. Igual que con las fórmulas para las expresiones lógicas, hay múltiples algoritmos para aplicar este proceso, diferenciándose entre ellos en la facilidad de implementación, la precisión y el coste de computación. Estos son unos de los algoritmos más usados:

Centroid Method: El método del centroide calcula el centro de masa del fuzzy set para determinar el valor preciso. Se considera uno de los métodos de defuzzificación más precisos, pero puede ser computacionalmente costoso.
Mean of Maximum (MOM) Method: El MOM encuentra la media del valor máximo del fuzzy set. Es relativamente fácil de implementar y computacionalmente económico, pero puede no producir siempre los resultados más precisos.
Weighted Average Method: El método de promedio ponderado encuentra la media de múltiples fuzzy set asignando pesos a cada uno de ellos. Este método es relativamente fácil de implementar y computacionalmente económico, pero puede no producir siempre los resultados más precisos.

El siguiente es el pseudocódigo para el algoritmo de Weighted Average Method, el cual es adecuado para un videojuego dado que es fácil de computar e implementar. Supone que se utiliza la función del trapezoide como función de membresía. El argumento de entrada fuzzySets es un vector en el que cada elemento es un struct que contiene el valor de membresía y los valores adecuados para computar la función del trapezoide:


function defuzzifyWeightedAverage(fuzzySets) return crispValue
	numerator ← 0.
	denminator ← 0.
	for each set in fuzzySets do
		center ← (set.left_peak + set.right_peak) / 2.
		numerator ← numerator + set.membershipValue * center
		denominator ← denominator + set.membershipValue
	if denominator == 0. then
		return 0.
	else
		return numerator / denominator

El conjunto de fuzzy sets que se inserta como argumento a la función de defuzzify deben de corresponder al mismo concepto. Por ejemplo, dada una supuesta acción de “curar compañero” que has definido con los fuzzy sets de low, medium y high, son esos 3 los que deberías de insertar juntos para que te proporcione un valor real de salida.

Un ejemplo de uso

Ahora que hemos definido todas las partes de un sistema de fuzzy logic, vamos a diseñar la inteligencia artificial de un personaje con el rol de healer. Para todos sus sensores y acciones, se crean 3 fuzzy sets para cada uno de ellos (low, medium, high). Son los siguientes:

Companion health: Sensor para la vida de un compañero del healer
Enemy fire resistance: Sensor que determina la resistencia del enemigo al fuego
Heal: Acción para curar a un compañero
Use fire buff: Acción que aplica daño de fuego a un compañero
Attack: Acción para atacar al enemigo

Y las siguientes son las reglas:

low_health → high_heal
medium_health → medium_heal
high_health → low_heal
low_fireResistance → high_fireBuff
medium_fireResistance → medium_fireBuff
high_fireResistance → low_fireBuff
low_health or low_fireResistance → low_attack
medium_health and medium_fireResistance → medium_attack
high_health and high_fireResistance → high_attack

Cuando se quiera realizar la inferencia, el primer paso es normalizar los valores de entrada, para luego aplicar fuzzification de los valores de fire resistance y companion health a sus respectivos fuzzy sets. A continuación, se computa en orden las reglas, y por último se aplica defuzzification de los fuzzy sets de salida a los valores reales que corresponden a las acciones de fire buff, heal y attack. Para seleccionar cuál de esas acciones ejecutar, simplemente se escogería el que tuviera el mayor valor.

Extensiones

Una primera extensión que se le puede ocurrir a un diseñado es darle más prioridad a una acción respecto a otras. En el ejemplo anterior, el healer podría desear el darle más importancia el mantener la vida de su compañero antes que aplicar un buff, dado que esa es la función principal de un healer. Para ello, solamente es necesario modificar las funciones de membresía para que el fuzzy set deseado ocupe una mayor área en el dominio, como se muestra en la siguiente imagen:

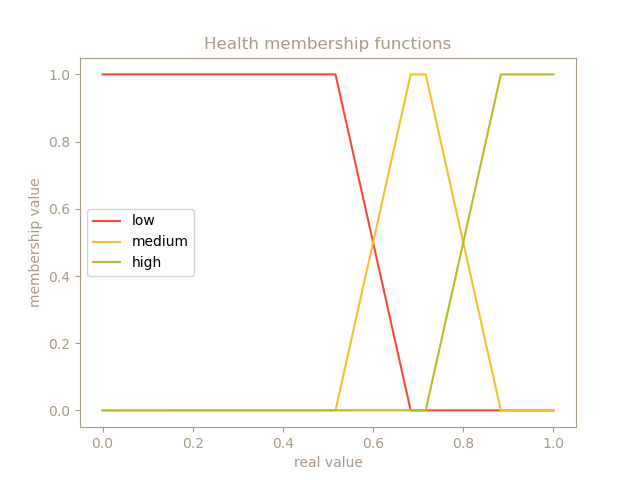
health_priority

Dado que el fuzzy set de low health ocupa una mayor parte del dominio, es más probable que se ejecute la acción de curar al compañero incluso si tiene una cantidad moderada de vida. El siguiente pseudocódigo incluye la modificación para crear los fuzzy sets con distintas áreas en el dominio (la suma de todos los weights debe de ser 1.):


function createTrapezoidalFuzzySetsWithWeights(fuzzySetCount, overlappingAmount, weights) return list
    listOfTuples ← empty list
    leftPeak ← null
    rightPeak ← null
    leftBound ← null
    rightBound ← null
    currentDx ← 0.
    overlap ← overlappingAmount / (fuzzySetCount * 2)
    for i ← 0 to fuzzySetCount do
        if( i == 0):
            leftBound ← 0. - 0.01
            leftPeak ←  0.
        else:
            leftBound  ← currentDx - overlap
            leftPeak   ← currentDx + overlap
			currentDx ← currentDx + weights[i]
        if(i >= fuzzySetCount - 1):
            rightBound ← 1.01
            rightPeak  ← 1.
        else:
            rightBound ← currentDx + overlap
            rightPeak  ← currentDx - overlap
        listOfTuples.add((leftBound, leftPeak, rightPeak, rightBound))
    return listOfTuples
end function

Otra extensión que un diseñador podría desear es la inferencia con múltiples objetivos. El ejemplo anterior solo tiene en cuenta que existe un compañero y un enemigo, pero pueden existir varios. Para añadir esa funcionalidad solamente hay que ejecutar las reglas múltiples veces, una para cada compañero/enemigo que hay en el entorno. El personaje seleccionaría la acción con un mayor valor entre todas ellas.

Para más detalles sobre la implementación y uso de un sistema de fuzzy logic, he creado un repositorio en github en el que lo implemento en C++.